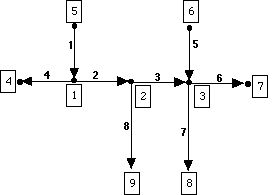
Lines are stored as arcs. Each arc starts and stops at a node. Because the arc starts and stops at a node, the arc has direction, defined by which node is the from node (FNODE) and which node is the to node (TNODE).... Consider the following sketch of arc-node topology, and fill out the table that follows (nodes are indicated by boxed numbers, arcs by unboxed numbers).

ARC
|
From
Node
|
To
Node
|
| 1
|
5
|
1
|
| 2
|
1 |
2 |
| 3
|
2 |
3 |
| 4
|
1 |
4 |
| 5
|
6 |
3 |
| 6
|
3 |
7 |
| 7
|
3 |
8 |
| 8
|
2 |
9 |
Arcs form the boundaries of polygons. The topology of a polygon coverage contains both an ID# for each arc and the identification of the polygon bounded on the right (RPOLY) and left (LPOLY) of the arc.... Consider the following sketch of polygon-arc topology, and fill out the table that follows (polygons are indicated by boxed numbers, arcs by unboxed numbers).
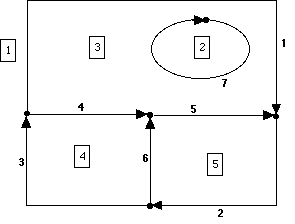
Also, consider arc ID#1. How does this arc turn two corners without have nodes at these corners?? The corners in Arc 1 are vertices that define the shape of the arc, rather than starting/ending nodes that would constitute new arcs.
POLY
|
#
of ARCS
|
ARCS
|
| 2
|
1
|
7
|
| 3
|
4 |
1, -4, -5, 7 |
| 4
|
3 |
3, 4, -6 |
| 5
|
3 |
2, 5, 6 |
ARC
|
Left
POLY
|
Right
POLY
|
| 1
|
1
|
3
|
| 2
|
1 |
5 |
| 3
|
1 |
4 |
| 4
|
3 |
4 |
| 5
|
3 |
5 |
| 6
|
4 |
5 |
| 7
|
3 |
2 |